6.3 아날로그의 디지털화(ADC)와 복호화(復號化: DAC)
원래 자연적인 아날로그신호는 송·수신을 한다거나 영상합성작업 등 어떤 처리과정에서 손실을 방지하기 위해 디지털로 변환시켜 처리 한다. 앞으로 TV방송 영상과 음향 관계를 중심으로 이야기하겠다. 영상의 컴포지트 신호나 컴포넌트 신호를 디지털화하는데 별문제가 없지만 처리과정에서 컴포넌트 영상신호를 선택하는 것이 보다 유익하다고 생각하여 현재 대부분은 컴포넌트 신호를 선호한다.
영상화면을 디지털화 하는 방법에는 크게 두 가지로 구분할 수 있는데 원래 컴포지트 영상신호인 R, G, B와 컴포넌트 색차신호인 Y, B-y, R-y(유럽에서 Y, U, V로 명명) 중에서 후자를 택하게 된 이유를 살펴본다.
6.3.1 컴포넌트 디지털신호의 선택 이유
TV방송 영상에서 사용되고 있는 컴포지트(Composite) R, G, B 신호가 아닌 컴포넌트(Component) 신호인 Y, B-y, R-y 신호를 표본화(Sub sampling)하고 양자화 하여 8bit와 10bit, 12 bit 등으로 바꾸어 압축하고 사용하는데 처음에는 8bit 신호로 만들어 압축하는 방식을 많이 사용돼왔으나 디지털의 발전으로 해상도를 높이기 위해 10bit, 12 bit, 14 bit 등을 택하게 된다.
8 bit를 사용하면 아날로그신호를 최대 256단계로 세분하여 디지털화할 수 있고, 10 bit는 아날로그신호를 1024단계로 세분하여 디지털화하는 데 매우 정교하게 처리된다.
1. Y, B-y, R-y 신호의 양자화에 유리
아날로그 영상신호를 디지털신호로 변환할 때 R, G, B 신호와 Y, B-y, R-y 신호의 표본화를 양자화 하는 데서 차이가 난다. R, G, B 신호는 Y, B-y, R-y 신호보다 벡터로 볼 때 신호의 크기가 짧기 때문에 양자화에서 에러(Error)가 발생하기 쉽다. 따라서 Y, B-y, R-y 신호의 양자화가 더욱 유리하다. 그러나 해상도에서 보면 반대로 R, G, B 신호 쪽이 디지털변환 후 더 좋다.
그래서 해상도를 높이기 위해 Y, B-y, R-y를 표본화하고 양자화를 10 bit 이상으로 높여 줄 필요가 있다. 앞서 설명했듯이 8 bit가 2의 8승으로 256단계를 갖는 반면 10 bit는 2의 10승으로 1024단계를 갖게 되어 정밀한 표본화와 양자화를 이룩할 수 있어 10 bit 사용은 R, G, B 신호만큼의 해상도를 유지할 수 있게 된다.
2. 크로마 데이터(Chroma Data)의 대역폭 축소 유리
R, G, B 영상신호를 사용할 경우 각각의 신호 대역폭이 5.5MHz를 갖기 때문에 전체의 영상신호 대역폭이 16.5MHz를 갖게 되나 Y, B-y, R-y 신호는 Y=5.5MHz, B-y=2.75 MHz, R-y=2.75MHz의 대역폭으로 충분하게 사용할 수 있어 전체적인 영상신호 대역폭이 11MHz로 축소된다. 따라서 데이터의 전송방법, 기록속도, 액세스 타임 등등에서 매우 유리하다.
그리고 아날로그 형태에서 R, G, B 신호를 Y, B-y, R-y 신호로 변경시키는데 저항(Resistor)을 이용한 매트릭스(Matrix) 회로의 구성으로 쉽게 만들 수 있다. 또한 필요할 경우 원래 영상신호인 R, G, B 신호로 복귀시키는데 어려움이 없다.
▲ 아날로그신호의 디지털신호로 변환 과정 복귀 단계
(1) 표본화(Sampling: 標本化)
(2) 양자화(Quantization: 量子化)
(3) 부호화(Encoding: 符號化): 디지털화
이러한 3 단계를 통하여 아날로그신호는 디지털신호로 변환될 수 있다. 그리고 우리가 영상신호를 알아보기 위해 디지털화된 신호를 풀어서 아날로그신호로 환원시켜야 하는 작업이 반드시 필요하다.
(4) 복호화(Decoding: 復號化)
(5) 저역 필터(Low Pass Filter)처리로 원래의 아날로그신호로 복귀한다.
이상과 같은 과정을 통하여 우리는 아날로그신호를 디지털신호로 그리고 다시 최후에 다시 아날로그신호로 전환을 활발히 사용하게 된다. 다시 한 번 자세하게 정리한다면 먼저 아날로그신호를 표본화하기 위한 High Cut Filter를 사용하고 영상신호의 상한선을 정하여 돌출되는 영상신호는 생략하도록 한다. 이때 영상신호의 손실이 약간 일어난다.
아날로그신호의 일정한 주기(週期) 동안 샘플링(Sampling)하여 추출한 값을 반올림하고 정해진 레벨의 단계를 만들어 2 진수(進數)로 수치화시키기 위한 작업을 양자화(量子化: Quantization)라 한다.
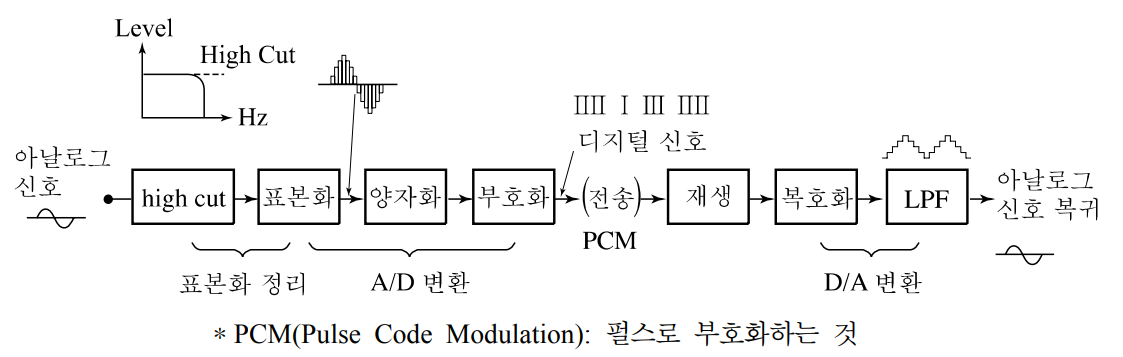
그림 6-2 A/D, PCM, D/A의 기본 변화 과정
그리고 양자화 된 것을 펄스(Pulse)로 변환시키는 것을 부호화(Encoding)라 하여 디지털신호 상태로 변환된다. 이렇게 디지털화한 신호는 전송이나 기록 등 여러 처리(Processing)를 거쳐 처음 표본화하기 이전의 아날로그신호 상태로 되돌려 놓기 위한 작업이 복호화(復號化)와 저역필터처리 작업이다.
다시 정리하면 처음 아날로그신호를 표본화하고, 부호화하고, 디지털신호로 변환하여 가공처리, 저장, 전송 등의 실행을 거쳐 결과를 확인하기 위해 복호화하고 원래의 아날로그신호로 환원한다.
그 과정에서 디지털을 아날로그신호로 D/A(Digital to Analog)변환에서 Low Pass Filter에 의해서 원래의 아날로그신호와 같게 매끄럽게 처리해 줌으로써 우리가 전송된 원래의 아날로그신호와 똑 같은 상태의 아날로그신호를 얻어 확인하고 인식할 수 있다.
6.3.2 표본화(Sampling)의 원리
표본화(標本化)는 샘플링 하는 행위를 말한다. 영속된 아날로그신호를 모두 사용하지 않고 일정한 시간간격으로 순간순간의 일정한 값(Sample: 수치)을 읽어 내어 처리하여 양자화한 후 디지털화 한다.
일례로 강물의 양을 측정하기 위해 흐르는 수로(水路)에서 수문(水門)을 일정한 시간간격으로 열었다 닫았다하면서 그때그때 물의 양을 측정한 값을 샘플링 하는 작업을 할 수 있다. 물이 많이 흘러들어올 때와 적게 들어올 때를 일정한 시간간격으로 측정한다.
이렇게 연속된 아날로그신호를 차례차례로 샘플링 해 가는데, 규칙적으로 시작해 약간의 지연시간을 일정하게 주어지게 되는데 이를 표준화 주파수라고 한다. 1 초간 동안 하나의 샘플을 택한다면 1Hz이다. 1 초에 1,000개의 샘플링을 한다면 1kHz가 된다.

그림 6-3 아날로그신호
이러한 원리로 표본화하지만 여기서 중요한 것은 아날로그신호를 어느 정도의 주파수로 샘플링하면 좋은가? 샘플링 주파수를 증가하면 원래신호에 가까운 신호를 선택할 수 있으나 그렇게 되면 데이터 용량이 아주 많아진다.
사논(Shannon)의 샘플링 정리에 의하면 표본화 주파수를 결정하기 위해 아날로그신호에 포함된 주파수 성분을 분석하고 그 주파수의 최고주파수를 라 할 때 그 의 2배 이상으로, 즉 2 이상의 주파수로 샘플링 한다면 원래신호를 복원할 때 매우 좋은 결과를 얻어낼 수 있다는 실험결과를 얻었다.

그림 6-4 표본화(sampling)
일례로 비디오보다 좀 간단한 디지털음향의 샘플링을 보면 보통 48kHz를 샘플링 주파수로 사용하게 되는데 그 이유는 우리가 0∼24kHz까지의 아날로그 음향주파수를 사용하고 있다. 따라서 최고 주파수인 24 KHz의 2배인 48 KHz가 Sampling 주파수로 결정된다.
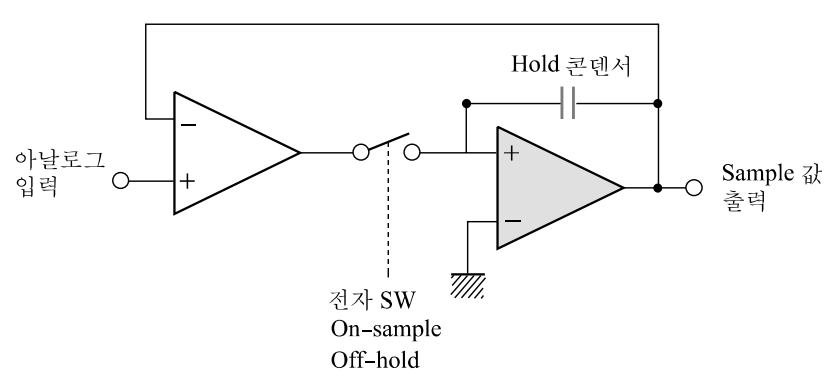
그림 6-5 표본화 출력회로의 일례
그림 6-5는 표본화할 때 사용될 수 있는 일종의 회로를 보여준다. 전자 스위치를 일정한 간격으로 열고 닫아 입력되는 아날로그신호의 샘플링 값을 얻어내는 사례이다.
6.3.3 양자화(Quantization: 量子化)
표본화에서 얻어진 샘플은 아직 아날로그신호를 단순히 표본화주기로 만들어 얻어냈을 뿐이고 아직도 아날로그 값에 불과하다. 양자화(量子化)란 Sampling값을 디지털신호로 변환하기 위해 더 이상 수치화할 수 없는 정수의 최소단위의 값으로 만드는 작업이 필요하다. <그림 6-4> 표본화에서 샘플 값인 4.2, 6.8, 3.3, 3.0, 6.0, … 10.0 등은 아날로그인 출력 파형의 순간 값에 불과하다.
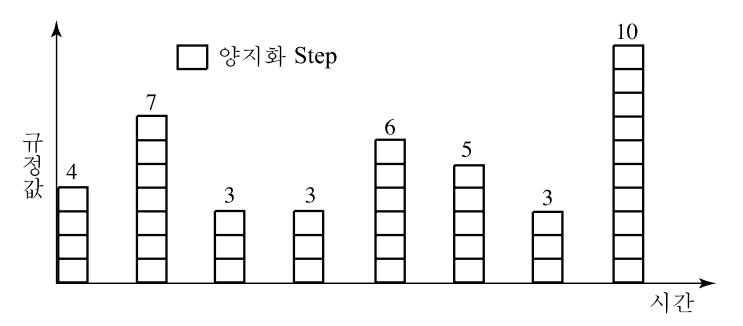
그림 6-6 양자화 단계 값
이것은 시분할(時分割)된 상태의 PAM(Pulse Amplitude Modulation)신호로 양자화 할 수 없다. 좀 더 자세히 설명하면 디지털에서 소수점을 인정할 수 없어 4.2, 6.8, 3.3, 3.0, 6.0, 5.1, 2.5, 10.0의 Sampling 값을 반올림하면 4, 7, 3, 3, 6, 5, 10의 양자화 값을 얻게 된다.
그런데 샘플링 진폭의 최대 값을 어떻게 정하고 세분하느냐에 따라서 그만큼 더 자세히 디지털화하기 위한 양자화가 쉽게 정해질 수 있다.
2진수로 표현할 수 있는 bit 수가 나타낼 수 있는 단계에 대한 개념을 먼저 알아보자!
1bit로는 0, 1인 2단계
2bit로는 00, 01, 10, 11인 4단계
3bit로는 000에서부터 최대 111까지 8단계
4bit로는 16단계
8bit로는 256단계
10bit로는 1024단계
12 bit로는 4096 단계
14 bit로는 16,384 단계
16bit로는 65,536단계까지 나타낼 수 있다.
이러한 단계(Step)의 bit를 크게 선정할수록 양자화의 오차는 작아진다. 디지털로 교체하기 위한 양자화 방법에서 몇 bit로 디지털화할 것인지 결정해야 한다. 일례로 8 bit, 10bit, 12bit 등의 결정에 따라서 양자화 값이 정해진다. 영상이라면 최대 밝기인 White 값이 양자화 값의 최고가 될 것이다. 8 bit 선택이라면 255, 10 bit라면 1024, 12 bit라면 4096이 된다.

그림 6-7 10을 최대진폭으로 계수화
오늘날 10 bit, 12 bit 등을 많이 채택하고 있지만 이해를 돕기 위하여 먼저 8bit의 경우를 하나의 예로 들어 설명한다. 8bit는 2의 8승으로 0∼255 단계까지샘플링 값을 세분해 양자화 할 수 있다.
위에서 샘플링 작업된 최대진폭 값 10(High Cut 값)을 8 bit의 최대 값인 255로 대응시키게 된다. 따라서 4.2의 대응 값은 10:255=4.2:X로 계산하고, 소수점 이하에서 반올림하여 보면 X=107.1 → 107이 양자화 값이 된다.
같은 방법으로 계산하고 정리하면
4.2 → 107
6.8 → 173
3.3 → 84
3.0 → 77
6.0 → 153
5.1 → 130
2.5 → 64
10.0 → 255로 대응된다.
이러한 결과는 8bit를 이용해 양자화 시킬 각 단계의 값을 찾았다. 이들 10진수를 2진수로 교체해 보면
107 /173 /84 /77 /153 …
01101011 /10101101 /01010100 /01001101 /10011001 … 이 된다.
10 진수를 2 진수로 변환하는 방법의 쉬운 과정을 한 번 찾아보자!
예를 들어 어떤 항아리에 담겨 있는 물의 용량을 측정하기 위하여 이미 알고 있는 단위의 여러 용기를 이용해 측정하는 방법이다. 8 bit라 하면은 다음과 같은 8개의 측정용기를 사용할 수 있다고 할 수 있다. 구체적으로 측정단위 용량을 보면 1(=2°), 2(=2¹), 4(=2²), 8(=2³), 16, 32, 64, 128인 8개의 용기를 사용할 수 있다. 즉, 8bit에 대응되는 10진수의 측정값을 준비해 8개 항아리로 수량을 측정해 2진수로 전화한 값을 만든다.
최소단위 용량인 1의 용기부터 측정한다면 여러 번 측정을 실행해야 하고 많은 시간이 필요할 것이다. 그러나 거꾸로 가장 큰 용기부터 적용해 측정한다면 몇 번의 측정으로 짧은 시간 안에 작업을 끝낼 수 있다. 다시 말하면 가장 큰 용기로부터 시작해서 작은 용기로 교체하면서 측정한다면 매우 빠르고 정확히 측정할 수 있다.
위의 예에서 107의 샘플링 된 수치를 측정하여 2진수로 교체하는 방법을 쉽게 찾아보자! 앞서 본바와 같이 8 bit인 경우 8개 용기를 준비할 수 있다. 그 중 제일 큰 것부터 순서대로 실행해 본다. 107에 대해 살펴본다면
1. 107은 128의 용기로 측정할 수 없어 실행하지 못하고 결과는 (0)
2. 64의 용기로 측정할 수 있으며 (1) 나머지는 43
3. 나머지 43은 32의 용기로 측정하고(1) 나머지는 11
4. 나머지 11은 16의 용기로 측정이 안 되어 (0)
5. 나머지 11은 8의 용기로 측정하고 (1) 나머지는 3
6. 나머지 3은 다음의 4의 용기로 측정할 수 없고 (0)
8. 나머지 3은 2의 용기로 측정하고 (1) 나머지는 1
9. 나머지 1은 1의 용기로 측정하여 (1) 끝이 난다.
이 결과를 차례로 정리해 보면 0110 1011이라는 8 bit에 대한 107의 2진수를 얻어낼 수 있다. 따라서 아날로그 10진수의 107은 2진수 0110 1011로 양자화 됐다고 할 수 있다. 매우 쉽고 논리적이다. 이렇게 쉽게 10진수를 2진수로 바꿀 수 있다.
그런데 그 후 처리과정에서 2진수로 처리하는 것보다 16진수로 처리하면 더욱 간단히 표시할 수 있고 빠른 속도로 처리할 수 있다. 다시 말해 0과 1을 8개씩 묶어 처리하는데 매우 번잡하고, 틀리기도 쉽고, 틀린 것을 찾아내기도 쉽지 않아 그보다 표현이 간편한 2진화 16진수로 변환하여 사용하면 매우 편리하고 좋다는 것을 알 수 있다.
16진수의 최대값 16은 24인 지수형태로 돼 있어 4bit씩 나누어 대응되는 것을 알 수 있다. 2진수를 4자리씩 취해서 16진수로 대응시켜 준다. 따라서 (107)10=(0110/1011)2=(6B)16의 관계로 간단히 표현된다.
여기에서 알 수 있듯이 4bit씩 2 부분으로 구분하여 0110/1011을 16진수인 6B로 코드화하여 취급하는 것이 매우 단순화되어 알아보기도 쉽고 처리속도도 매우 빨라진다. 구체적으로 0110/1011의 2진수를 16진법으로 표시된다면 앞의 (0110)2 =(6)16, 뒤의 (1011)2=B가 되어 6BH로 간단히 표시된다. 여기서 H의 표시는 16(Hexadecimal) 진수의 의미의 갖고있다.
16진수 표시방법을 이용하여 10진수의 0은 00H, 1은 01H, 2는 02H 등과 같이 2자리로 표시한다. 역으로 16진수에서 10진수로 쉽게 변환할 수도 있다. 일례로 16진수 6BH → 10진수로 (6×161+11×160)= 107이 된다.
표 6-1 2진화 16진수 변환 관계
| 10진수 | 2진화16진수 | 2진수 → 16진수 | 2진수 → 16진수 | |||
| 107 | 6BH | 0110 | 6 | 1011 | B | |
| 173 | A8H | 1010 | A | 1000 | 8 | |
| 84 | 54H | 0101 | 5 | 0100 | 4 | |
| 77 | 4DH | 0100 | 4 | 1101 | D | |
| 153 | 99H | 1001 | 9 | 1001 | 9 | |
| 130 | 82H | 1000 | 8 | 0010 | 2 | |
| 64 | 40H | 0100 | 4 | 0000 | 0 | |
| 255 | FFH | 1111 | F | 1111 | F | |
표 6-2 10진수, 2진수, 16진수의 관계
| 10진수 | 1 | 2 | 3 | 4 | 5 | ~ | 10 | 11 | 12 | 13 | 14 | 15 |
| 2진수 | 0001 | 0010 | 0011 | 0100 | 0101 | ~ | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
| 16진수 | 01H | 02H | 03H | 04H | 05H | ~ | 0AH | 0BH | 0CH | 0DH | 0EH | 0FH |
이러한 이론을 바탕으로 아날로그의 신호를 16진수의 양자화 후 디지털신호로 변환해 주는 변화장치가 「축차비교형(逐次比較形) A/D 컨버터」라고 한다. 물론 이러한 방법은 여러 디지털 변환방법 중에서 하나의 일례에 불과하다. 그 외에도 여러 가지 좋은 디지털화 방법이 개발되고 있다.
지금까지의 설명에서 아날로그의 값을 디지털화하는데 반드시 샘플링, 양자화 과정에서 약간의 오차가 있다는 것을 감지할 수 있다. 양자화과정에서 Sampling의 최고점인 High Cut 결정과 샘플링 스텝(Step)을 몇 bit로 결정할 것인가에 따라 오차범위가 결정될 수 있다. 높게 bit 값을 설정한다면 할수록 오차가 작아지지만 오차가 전혀 없게 할 수는 없다.
다시 말하면 아날로그신호를 디지털신호화 하는 과정에서 약간의 손실이 발생하고 다음에 설명할 디지털신호를 아날로그신호로 원상회복하는 복호화(復號化)작업에서도 약간의 손실이 발생한다. 다만 아날로그신호를 그대로 사용할 때보다 매우 미미한 손실이라고 할 수 있다.
여기에서 알 수 있듯이 A/D, D/A로 변환작업이 많으면 많을수록 신호의 손실, 즉 열화가 발생한다는 것을 알 수 있다. 따라서 제작과정에서 아날로그신호를 디지털신호로, 디지털신호를 아날로그신호로 여러 번 교체하면서 작업이 이루어지는 환경에서 영상편집을 행하거나 합성작업을 한다면 특히 높은 주파수인 컬러의 손실이 많아진다.
6.3.4 부호화(디지털신호) 작업
양자화 된 수치를 부호화하여 저장하고 송·수신하는 처리(Processing) 과정이 필요하다. 아날로그신호를 2진수 0, 1로 양자화 했지만 기계장치가 0, 1의 숫자를 인식할 수 없다. 따라서 이를 구형(矩形) Pulse 모양으로 바꾸어 주어야 하는데 이를 PCM(Pulse Code Modulation)이라고 한다. 이렇게 만들어져 완성된 구형 Pulse 신호를 디지털신호(Digital Signal)라고 하고, 이 과정을 부호화 작업이라고 한다.
구형 Pulse의 신호는 1인 경우 높게, 0인 경우 낮게 하여 구형으로 표현한다. 다시 말하면 아날로그신호가 표본화되고 양자화 되어 2진법으로 변환되고 이것이 구형 Pulse로 변환되어 기록되고, 전송, 재생(再生)되어 최종적으로 우리가 알아 보기위해 복호화 시킨 후 Low Pass Filter를 거처 원래의 아날로그신호와 유사하게 만들어 인식할 수 있게 한다.
그런데 부호화(符號化)하는 과정에서 디지털의 압축 기술이 필요에 따라서 요구되고 사용된다. 압축된 신호는 저장하거나 전송하기 편리하도록 처리된다. 압축은 다양한 기법을 이용하여 정보의 중복성을 이용하는 방법인데 한 가지 기법만으로는 항상 모든 것에 최선의 결과를 얻지 못한다. 따라서 디지털신호를 여러 가지 방법으로 압축하는 기술이 나날이 발전되고 있고 있다.
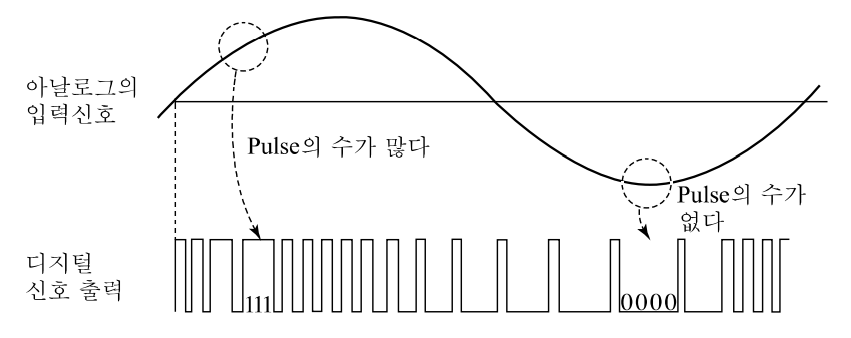
그림 6-8 PCM 디지털 부호화
6.3.5 복호화(復號化) 작업
일단 디지털신호로 입력된 신호를 우리가 가시화하기 위하여 원래의 아날로그신호 형태로 복귀시켜 주어야 알 수 있다. 이때 디지털화하기 전의 상태를 완벽하게 재현할 수 있다면 성공한 것이다. 그러나 완전한 복귀란 있을 수 없고 가장 가까운 근사 값에 접근할 수 있다.
디지털신호인 구형(丘型) Pulse신호를 2진수로 변환하고, 2진수를 10진수로 환원하여 양자화 이전의 단계로 변환하고 Sampling 값으로 환원한다. 이러한 작업을 D/A 변환이라고 한다. 간단히 D/A 컨버터 변환방법을 살펴보자!
변환기는 8bit용 A/D 컨버터를 이용하여 만들어진 디지털이기 때문에 20, 21, 22, 23, 24…, 즉 10진법에 대응되는 수는 1, 2, 4, 8, 16, 32, 64, 128, 각각 8개의 수치와 동일한 값을 갖는다. 이 0과 1의 정위수(定位數)를 찾아내어 합산하면 원래의 아날로그 양자화 값을 얻을 수 있다.
아래 표 6-3에서 최상위 bit인 MSB(Most Significant Bit)에 2진수 1이 들어 있으면 128의 출력이 생기고, 다음의 SB2에 2진수 1이 들어 있으면 64의 출력, SB3에 1이 들어 있으면 32의 출력, SB4에 1이 들어 있으면 16, SB5에 1이 있으면 8, SB6에 1이 있으면 4, SB7에 1이 있으면 2, 최하위 bit LBS에 1이 있으면 1의 출력이 발생한다. 이 8단계에 모두 1이 되어 있다면 모두가 가산되어 결과는 255가 된다.
표 6-3 2 진수를 10 진수로 변환
| 10진수 값 | 107 | 173 | 84 | 77 | 153 | 130 | 64 | 255 | 10진수 |
| 최상위비트(MBS) | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 128 |
| SB2 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 64 |
| SB3 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 32 |
| SB3 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 16 |
| SB5 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 8 |
| SB6 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 4 |
| SB7 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 2 |
| 최하위비트(LSB) | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
그리고 255가 10이라고 가정했다면 107은 약 4.2이고, 173은 약 6.8이고, ……255는 10이 된다. 원래의 아날로그 신호인 값과 약간의 차이가 발생하는 것은 양자화하고 복호화 하는 과정에서 일어난다.
6.3.6 저역 필터(Low Pass Filter) 작업
D/A 변환과정에서 디지털신호를 아날로그신호로 변환하면서 그 신호에 많은 고주파를 포함하게 되어 있어 이 불필요한 고주파를 제거하고 매끈한 원래의 아날로그신호에 아주 근접한 아날로그신호로 귀환하도록 하여야 한다.
이때 사용되는 저역 필터(Low Pass Filter)가 이러한 고주파를 제거하는 일을 하고 있다. D/A 변환 후 아날로그 출력은 그림에서 보는 바와 같이 처음 계단파형을 형성하고 많은 고주파를 포함하고 있는 것을 간단한 RC(Resistor–capacitor Circuit)필터를 사용하게 되면 매끄러운 원래의 아날로그 파형으로 복귀시킬 수 있다.
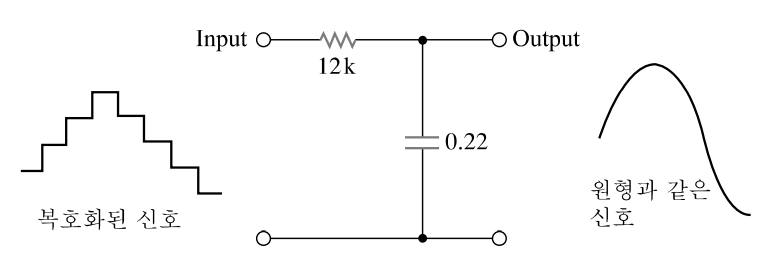
그림 6-9 low pass filter에 의해 원형 회복
최근 기술에 의해 복호화 과정에서 재생되는 계단파형을 보다 조밀하게 하는 방법이 이용되고 있다. RC 필터를 사용하는 방법도 아주 정밀한 원래의 신호를 복호화 하는 한 가지 방법이다.
그 외에도 영상의 화질(畵質을 어떻게 처리할 것인가에 따라서 여러 가지 Low Pass Filter(LPF), High Pass Filter(HPF)를 중간과정에서 여러 가지로 사용되고 있다.
6.3.7 영상 디지털신호의 압축
아날로그 영상신호를 디지털 영상신호로 변환하면서 새로운 도전과 여러 발전 가능성이 개발되고 있다. 아날로그의 영상신호를 압축해서 전송하거나 저장한다는 것은 상상도 할 수 없었다.
그러나 디지털화하면서 같은 값을 가진 데이터를 전송하거나 저장하는데 반복해 기록하고 전송할 필요가 없다. 일례를 들어 HDTV에서 전체의 영상이 완전한 흰색(White)이라면 각 디지털신호 1개의 픽셀(Pixel)은 R, G, B 각각 16진수로 FF/FF/FF를 표시할 수 있다.
이중에서 1 Line 주사선(Scanning Line)의 모든 정보를 전송이나 저장을 위하여 FF/FF/FF를 1920 픽셀에 대응되는 숫자만큼 1920번 반복해 사용하는 대신 FF/FF/FF x 1920 이라는 영상신호 데이터를 저장하거나 전송하는 것으로 충분할 수 있다. 이러한 방법이 일종의 디지털 압축방식이다. 압축의 메리트는 운용비용(Running Cost)과 유지보수 비용(Maintenance Cost)의 절감 등을 위해 다음과 같은 조건들을 만족하여야 한다.
① 영상이나 음향의 질이 높아야 한다.
② 영상의 움직임에 의한 영향이 없어야 한다.
③ 속도의 변화, 재생에 지장이 없어야 한다.
④ 편집점의 선택에 제한이 없어야 한다.
이러한 조건을 만족시키기 위해서는 압축 비율이 높은 것보다 낮아야 하지만 앞으로 기술의 발전에 따라서 해결될 수 있을 것이다. 영상의 압축은 주로 한 프레임(Frame)를 중심으로 이루어져야 편집점을 자유롭게 선택할 가능성이 있다. 새로운 디지털 압축방법이 속속 개발되고 있는데 그 중 몇 가지 방법을 소개하도록 한다.
1. 시간적 중복성(重複性)을 이용한 압축
일반적으로 TV방송 영상을 보면 1초당 30장(Frame)씩 연속적으로 변화를 갖고 있다. 따라서 매우 빠른 속도로 변화를 갖지 않는다면 서로 인접한 영상 간에는 시간적으로 많은 중복된 영상자료를 갖게 된다. 이 시간적 중복성을 이용하여 압축하는 방법을 프레임 간(間)(Interframe) 압축이라고 한다.
다시 말하면 1초당 30장의 그림을 연속적으로 전송해야 할 것을 연속된 프레임이나 필드 사이에 변화된 내용만을 축출하여 보내주고 공통된 데이터와 같이 사용한다면 상당한 전송 정보량을 줄일 수 있다.
이러한 방법이 있다면 완벽한 영상의 전달을 할 수 있게 된다. 왜냐하면 중복되는 정보량은 여러 번 전송할 필요가 없기 때문이다. 그러나 정적인 영상의 시간적 중복성을 이용한 압축방식에서 별문제가 없지만 빠르게 움직이는 영상의 정보 전달은 늦어져 부자연스럽게 되고 전송 중 오류가 발생하기 쉬워 전혀 다른 프레임 전달이 될 수 있다.
이를 연속 프레임 간에 이루어진다고 해서 프레임 간 압축(Interframe Compression)이라고 한다. 이 압축 기술은 연속적인 프레임 사이의 차이를 계산해서 휘도(Y)와 색차신호(B-y, R-y)의 정보를 전달한다. 휘도(Y)신호는 4개의 정보 블록과 색차신호 각각 2개의 정보 블록으로 샘플링하게 되는데 Y : B-y : R-y = 4:2:2로 정의하고 있다.
2. 공간적 중복성(重複性)을 이용한 압축
TV방송 영상화면의 한 프레임 중에는 많은 양의 공간적 중복성을 갖고 있는 경우가 많다. 파란 하늘, 흰 종이와 같이 어느 일정한 블록(8×8) 부분의 색상과 밝기는 동일하다. 따라서 이 부분을 구성하고 있는 화소(Pixel)들은 공간적으로 연관되어 있다. 이 화소들의 블록을 비교하여 동일한 휘도와 색차신호의 정보를 모두 보낼 필요가 없기 때문에 첫 번째 정보만 보내고 몇 번 반복되는지 그 정보만 보내면 된다.
복잡한 수학연산인 DCT(Discrete Cosine Transform)는 그 데이터 블록의 각 화소 값들을 시간영역에서 주파수영역으로 변환시킨다. 그 변화과정은 블록 내의 화소들 사이에 존재하는 연관성을 이용한다. 중간과정의 설명을 생략하고 결과적으로 서로 인접한 부분에 변화가 거의 없으면 주파수변환 후에 낮은 주파수 항들이 생성된다.
반면 화면의 변화가 심한 부분을 포함하는 부분은 주파수영역에서 높은 주파수 항이 많이 나타난다. 여기까지는 데이터의 어떠한 감소도 발생하지 않고 있으며, 다만 수학적인 연산에서 필수 불가결한 반올림에서 오는 손실밖에 없다.
디지털화하는 과정 중에 양자화가 필요한데 실제 데이터의 감소가 일어난다. 아날로그신호로 구성된 영상의 밝기는 많은 단계로 표시되겠지만 인간의 시각으로 약 256단계 정도의 표현이면 충분하다고 한다. 따라서 DCT 과정의 출력계수를 부호화하는데 필요한 값의 범위는 정해진 수의 단계로 제한될 수 있다.
간단한 예로 어떤 영상의 주파수영역으로 변환된 결과가 1.75, 3.42, 7.98 등이면 이들 집합을 만들 때 반올림하여 2, 3, 8 등으로 집합하여 양자화 한다면 더 적은 정보로 전달될 수 있다. 결론적으로 연속된 영상들 사이에 중복되는 데이터를 빼고 그 차이만을 전송한다. 이러한 압축은 여러 프레임을 비교한 것이 아니고 1프레임 내에서 생성되므로 프레임 내(內)압축이라 한다.
3. 통계적 중복성(重複性)을 이용한 압축
TV방송 영상화면에는 규칙적으로 반복되는 정보가 상당히 많이 포함되고 있다. 따라서 디지털신호에서는 아날로그의 Line Blanking, Field Blanking 신호를 전송할 필요가 없어 전송 데이터양이 줄일 수 있으며, 동기를 위하여 Line 동기, Frame 동기를 표시하는 코드만 전송하게 된다.
그 외에도 여러 가지 DCT, 양자화 등에서 만들어지는 데이터의 같은 값이 빈번하게 일어난다. 예로 영문자를 전송할 때 가장 빈도수가 많은 E자를 가장 짧은 bit(점 하나)로 부호화할 수 있다면 전송 데이터를 줄일 수 있다. 이러한 방법이 통계적 중복성(重複性)을 이용한 압축 기술이다.
소니 회사에서는 DCT(Discrete Cosine Transforms)를 베이스(Base)로 새로운 압축 기술을 채용하고 있다. 처음에 한 장의 그림을 격자(망) 모양으로 구획을 정하고 만들어진 블록(Block) 하나하나를 압축할 단위로 정한다. 이 작은 블록은 영상의 밝기와 색의 강약으로 되어 있으며, 영상의 종 방향과 횡 방향 각각의 파형집합으로 표시할 수 있다.
영상의 정보는 시간적인 변화로 표현하는 방법과 여러 가지 주파수와의 합성으로 표현하는 방법이 있으며, 시간영역의 표현으로부터 주파수영역의 표현으로 변환(Transform)하는 것이 DCT이다.
이렇게 영상을 DCT 처리를 함으로써 원래화소의 레벨 표현을 주파수 성분마다 계수 값으로 변환된다. 이렇게 되면 영상은 상당히 낮은 주파수에 해당하는 성분이 대부분이고 높은 주파수 성분의 에너지는 극히 적은 것을 알 수 있다.
따라서 고역 주파수 성분을 저역 주파수 성분보다 거칠게 표현하여도 인간의 눈은 시각 특성상 그 차이를 분별하기 어렵다. 이와 같은 특성을 이용하여 고역성분의 분해를 낮게 억제하는 것이 1단계 압축이다.
2단계 압축은 데이터의 압축이다. 얻어진 데이터 중 가장 많이 나타나는 데이터의 전송을 가장 작은 값의 신호로 처리한다. 우리가 영문에서 가장 많이 사용되는 글자가‘E’라 하고, 가장 적게 사용되는 글자는‘Q’라고 한다. E자 정보는 가장 간단한 비트신호를 사용하고, Q자 정보는 가장 큰 비트신호로 처리한다면 전체적인 신호처리 속도를 높일 수 있다. 영상에서도 같은 원리를 적용하여 전체 데이터 량을 억제할 수 있다.
대략적인 설명이지만 이것이 DCT에 의한 압축이다. 동일한 영상을 압축한 것을 다시 압축할 때 완전히 일치하도록 하고 있어 몇 번의 더빙(Dubbing)을 실행하여도 화질의 열화가 생기지 않는다.
'TV방송 시스템운용과 영상제작' 카테고리의 다른 글
| 06. 디지털 영상신호의 개념(5) (0) | 2021.03.16 |
|---|---|
| 06 디지털 영상신호의 개념(4) (0) | 2021.03.12 |
| 06 디지털 영상신호의 개념(2) (0) | 2021.02.25 |
| 06 디지털 영상신호의 개념(1) (0) | 2021.02.20 |
| 05. TV방송의 제작영역(3) (0) | 2021.02.13 |